In structural engineering, a modal analysis uses the overall mass and stiffness of a structure to find the various periods at which the structure will naturally resonate, along with the frequencies of vibration of the structure. In RISA-3D, the modal analysis is a prerequisite to the response spectra analysis, which uses these frequencies to calculate forces, stresses and deflections in the model.
When conducting a modal response spectrum analysis, building codes (including ASCE 7) require that a sufficient number of modes be used to understand the overall response of the structure. While it is not always possible to achieve full participation (a case where 100% of the modal mass is accounted for) the code does at minimum require that a modal analysis shall include a minimum number of modes in order to obtain a combined mass participation of at least 90% of the actual mass in each orthogonal horizontal direction (X & Z directions in RISA-3D).
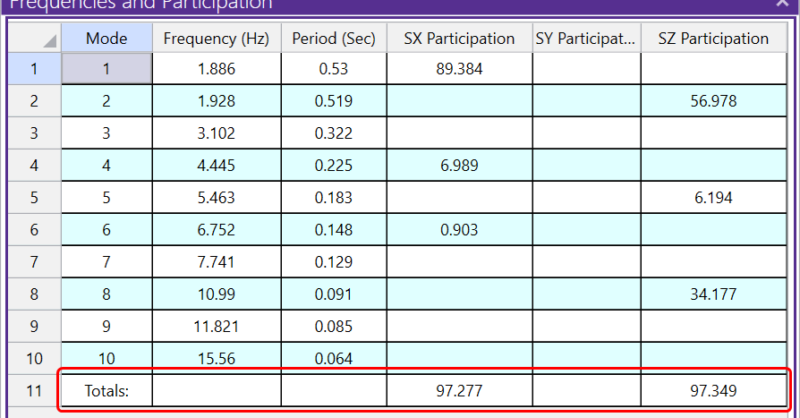
In order to determine the appropriate number of modes for a given structure (while also achieving the 90% mass participation required by code), RISA-3D users must first pick an arbitrary number of modes (5 to 10 is usually a good starting point) and solve the response spectrum analysis. If the model has not reached 90% mass participation (as shown in the image below), there are a variety of options users can utilize in order to improve mass participation above the required threshold.
Increase the Number of Modes
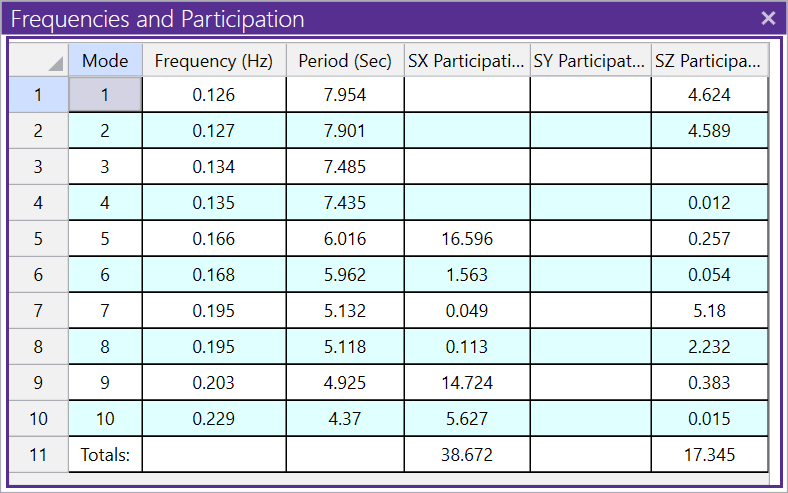
The simplest and most direct way to improve mass participation is by increasing the number of modes used in the dynamic analysis. Doing so will also increase the overall time it takes to complete the dynamic solution. When increasing the number of modes, you may notice that many of the modes have little or no mass associated with them. These “local modes” can cause further issues in the model if they aren’t dealt with accordingly.
Local Modes
Local modes are not immediately obvious when looking at the frequency or numeric mode shape results. However, they are easy to spot when using the mode shape animation feature found in the Animate section of the View toolbar.

Evaluating the animation for Mode Shape 4 (from the above table) we see that a local mode exists where only a small portion of the structure in one area is vibrating.
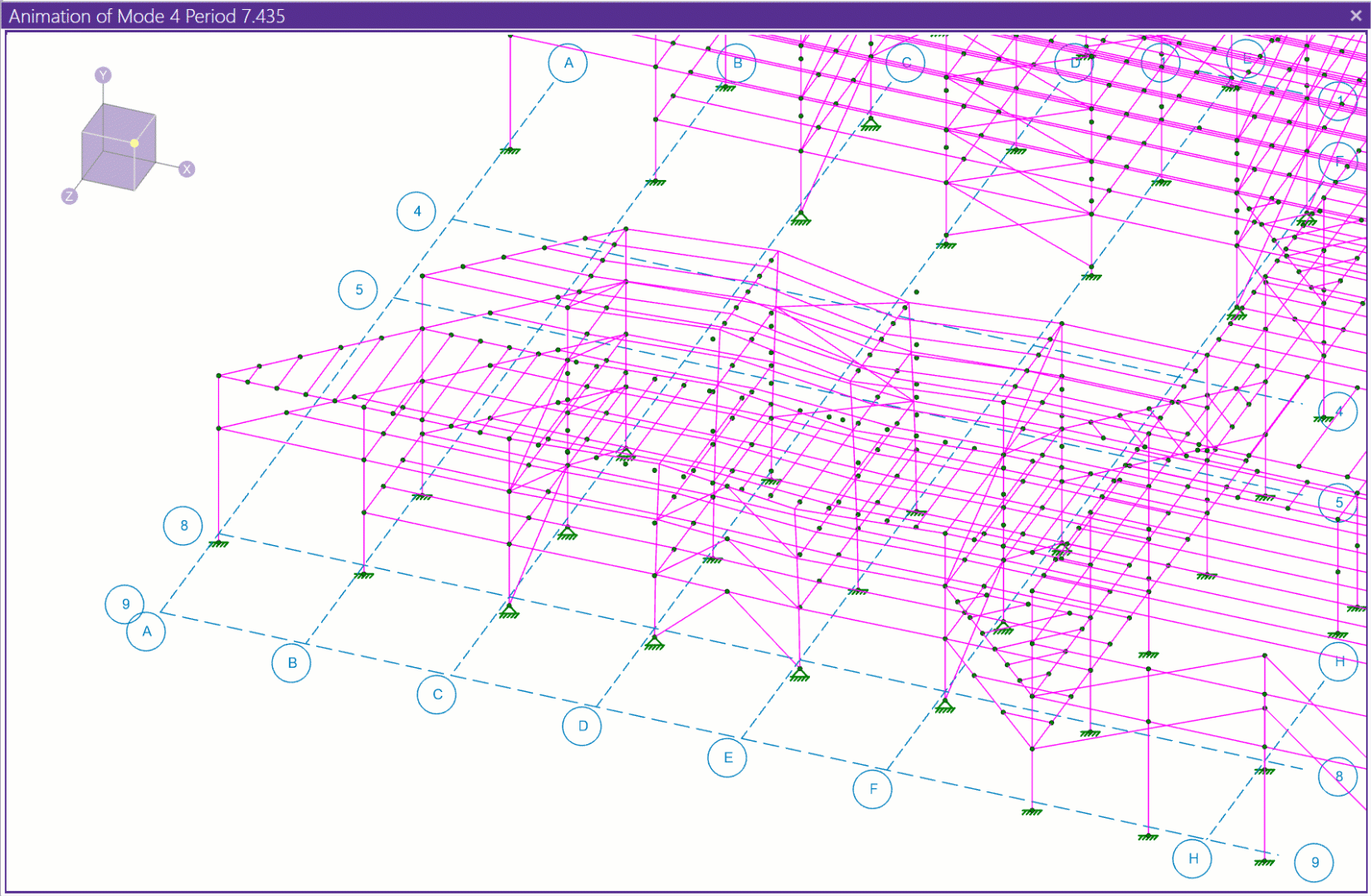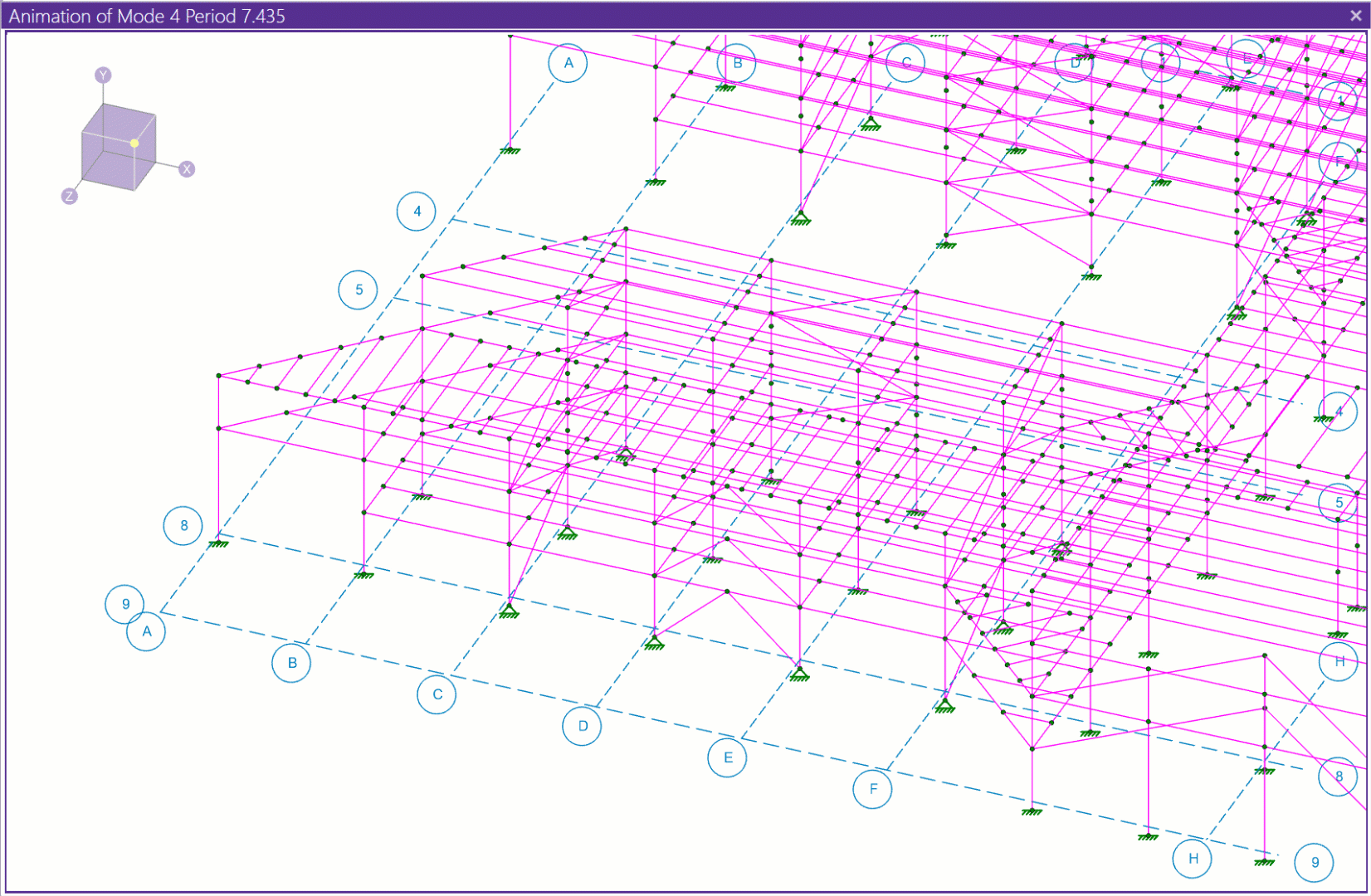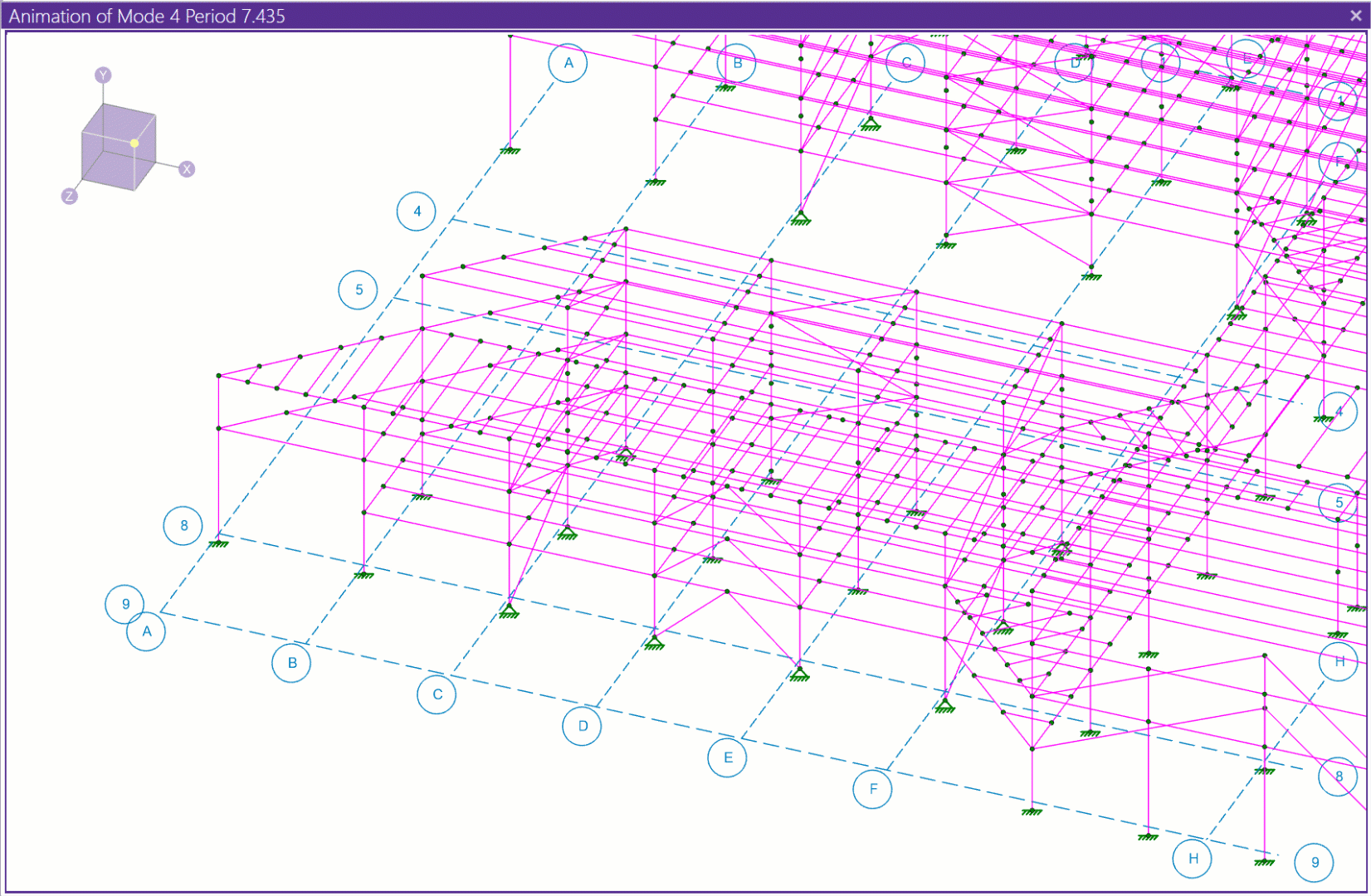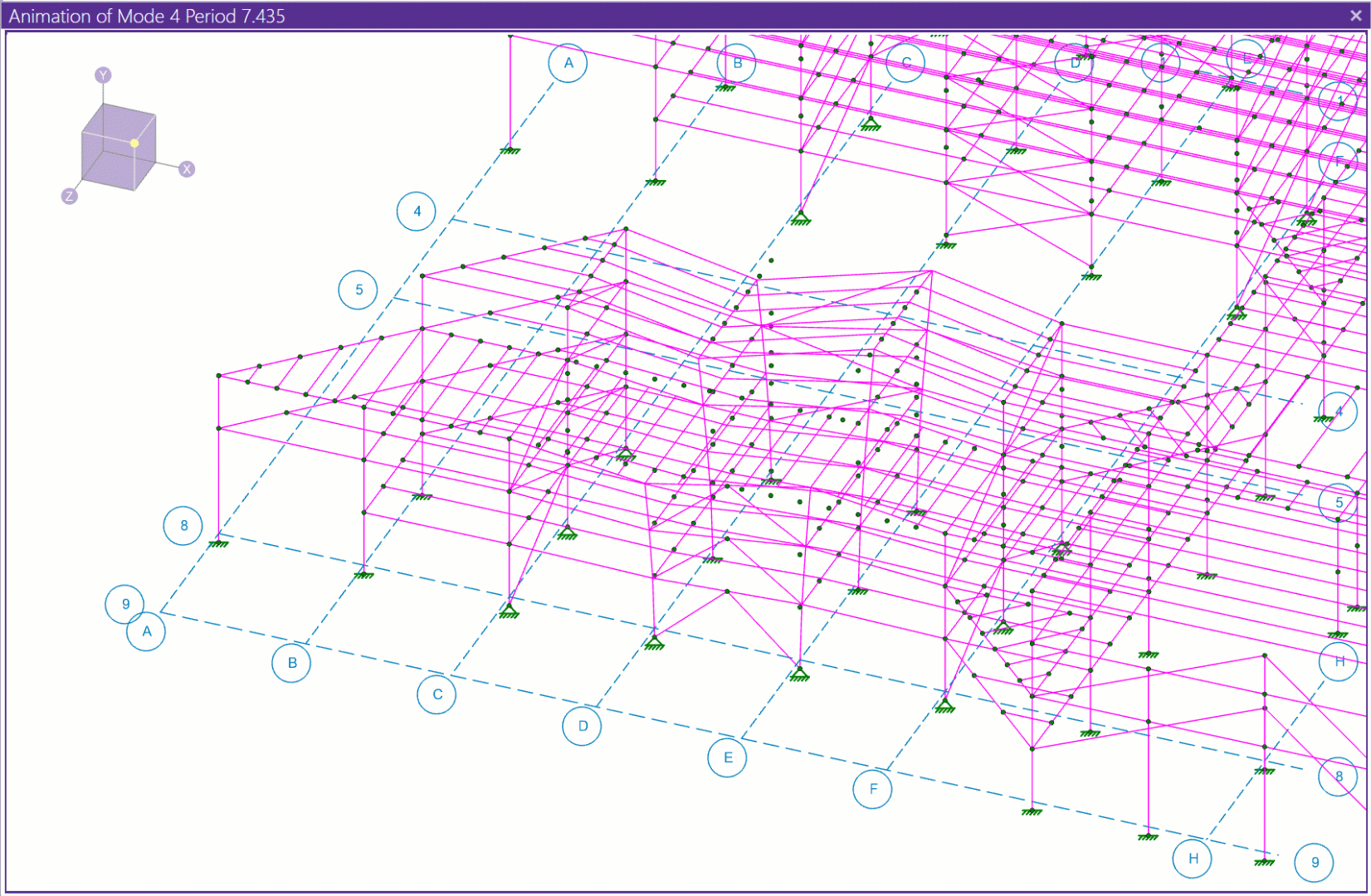
A localized mode like the one shown above can make it difficult to get enough mass participation in the response spectra analysis (RSA), since these local modes don’t usually have much mass associated with them. Quite often, localized modes are due to modeling errors (erroneous boundary conditions, members not attached to plates correctly, etc.). If you think this may be the case, running the Model Merge tool found in the Modify tab should be done before taking further action.
Eliminating Local Modes - Model
To eliminate localized modes that are not the result of modeling errors, you can sometimes use boundary conditions to restrain the mode shape. For example, if your localized mode is at a weak X brace, you could attach a spring to the center of the X brace to restrain the mode shape.
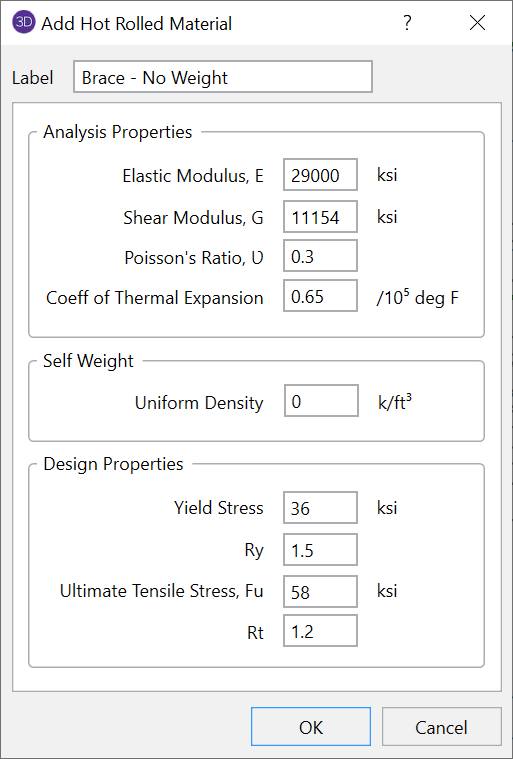
Another option for braces that are the cause of local modes is to eliminate their mass entirely by utilizing a weightless material. In this case no mass would be assigned to the X-brace intersection and it would not participate in the eigensolution.
Yet another option for braces requires the deletion of the node at the crossing of X-braces. If there is no node at this location there is no degree of freedom. This location will not likely be crucial for a dynamic solution anyway, so eliminating the node eliminates a flexible mode with minimal mass participation.
Eliminating Local Modes - Solver
Another cause of local modes is including the self-weight in models with walls or horizontal diaphragms modeled with plate/shell elements. These walls and floors can have many modes that will tend to vibrate out-of-plane like drums, but will have very little effect on the lateral seismic response of the structure. For cases like this it will often be better to switch from the standard or accelerated dynamic solvers to the Ritz Vector dynamic solver because Ritz vectors are inherently biased to avoid modes with little mass participation in the desired direction.
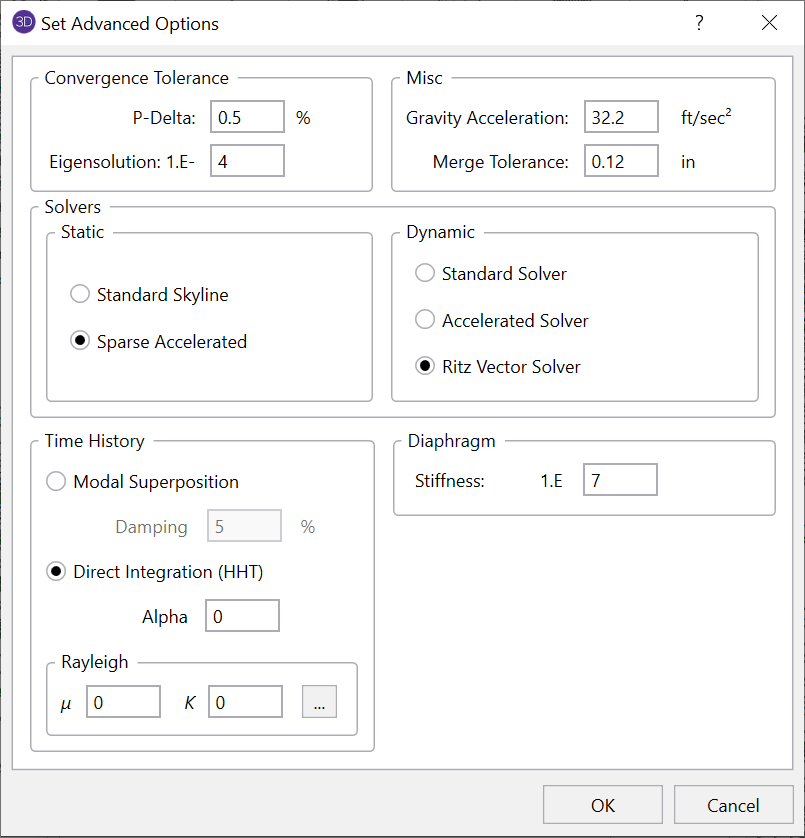
For more information about the Ritz Vector Solver, review the article listed below:
Residual/Missing Mass
Users can also utilize a structures "Residual Mass" to help improve the overall mass participation. Doing so is appropriate for structures that have a large amount of mass at the lower levels of the structure and where the mass is associated with very rigid modes. These modes may be so rigid that it may not be necessary to calculate the actual eigen modes. Instead, their response can be estimated accurately (and much more efficiently) using some simple estimates of their response. This is achieved by determining what mass has been activated already with the currently solved eigen modes. This tells the solver where “residual or missing mass” is that has not been activated. If one applies a response spectra acceleration equal to the zero period acceleration to this mass, then this should provide a reasonable estimate of the residual or missing mass. For a more detailed explanation of residual mass and how it is utilized within RISA-3D, visit the article listed below.