Products
Learn
Support
Company
RISA-3D continues to be at the cutting-edge of finite elements analysis software with the release of the Geometric Nonlinear Stiffness method for use during P-Delta analysis.
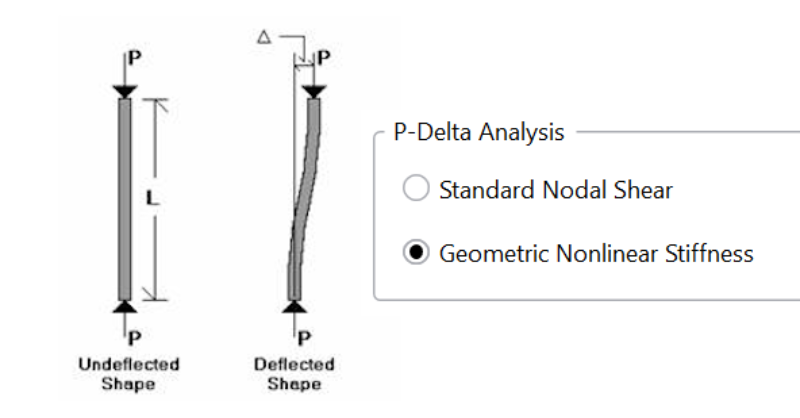
Traditionally, RISA-3D considered P-Delta effects using a Standard Nodal Shear methodology which applies pseudo shear loads at the individual member nodes based on the axial load, lateral deflection and member geometry. To select this method, navigate to Model Settings > Advanced.
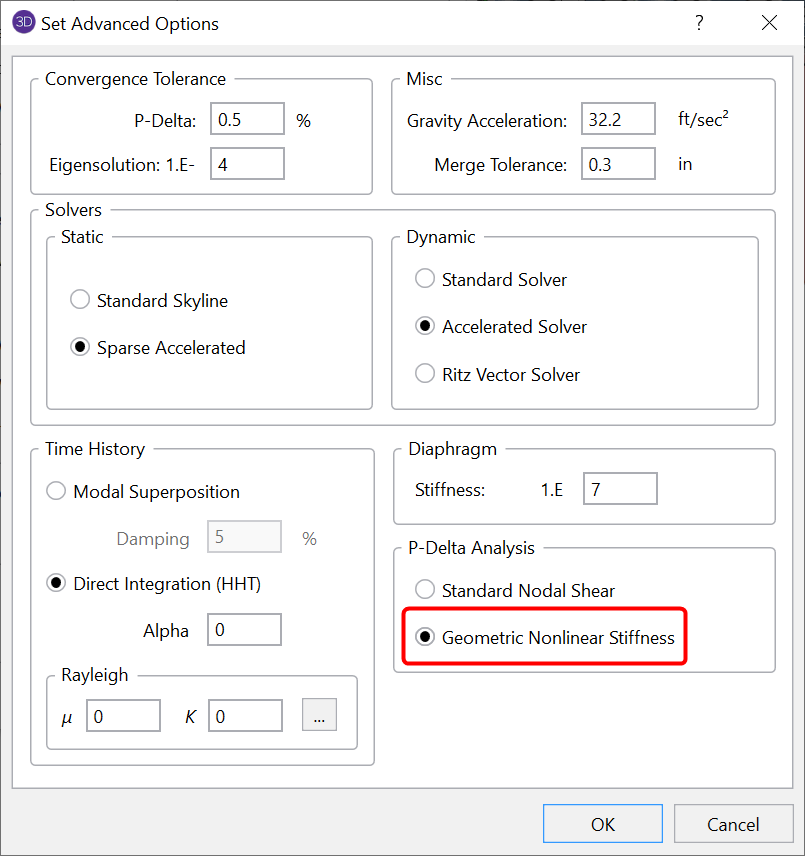
When comparing the two methods, the standard Nodal Shear Method has been used for many years when considering P-Delta effects in RISA-3D. It is a widely utilized methodology in evaluating the secondary effect of the structure and proved to have great performance in most cases. However, due to the limitations of the method itself, it diverges quickly when axial loads approach the buckling loads. As a result, the P-Delta divergence could potentially occur prematurely for some structures. Another limitation of this method is that the loading is node based, and due to this, users would have to manually add internal nodes along the member to properly consider the P-small delta effect.
For additional information on the Nodal Shear Method in RISA-3D and how it handles small P-Delta effects, visit our Online Help. Search Secondary P-Delta Effects.
Finally, the new method directly modifies the member stiffness matrix to account for the stiffness reduction due to the axial loads. Doing so, results in the following benefits in analysis:
Better convergence behavior, More suitable for P-Delta analysis of irregular/complex models
More accurate deflections with fewer nodes (small P-Delta included automatically)