How can I transition a Plate Mesh from Round to Rectangular?
Transitioning plates from a circular (or elliptical) to a square (or...
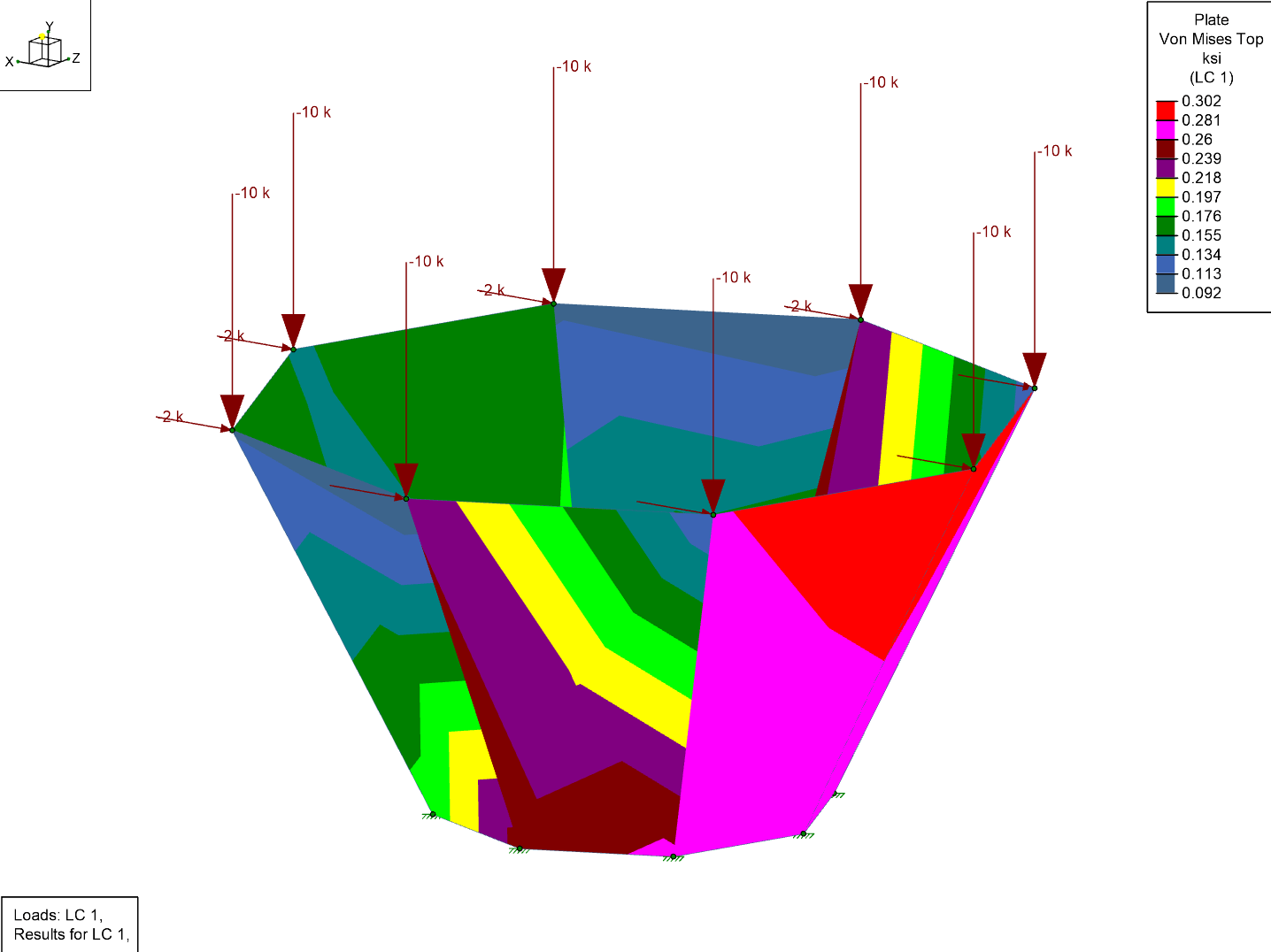
Aside from the topic of plate connectivity, the concept of plate meshing is equally important to the analysis of structures using finite elements (plates).
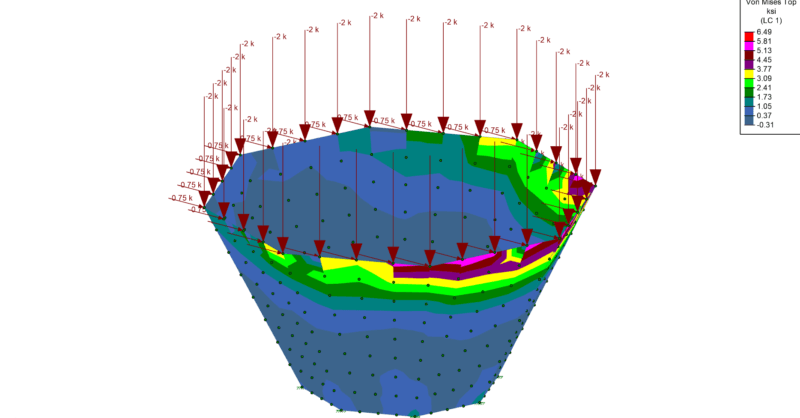
Submeshing the model above will only improve the results so much, because any submeshing will still leave the cone shaped octagonally. Instead the model has been completely regenerated below as a 40-sided cone with five plates vertically instead of just one.
The total load is still the same, but you can see that the stress contours are much smoother, and show more subtlety. Furthermore the maximum stress shown on the contours is now 846 psi, which is almost double what it was in the roughly meshed cone.
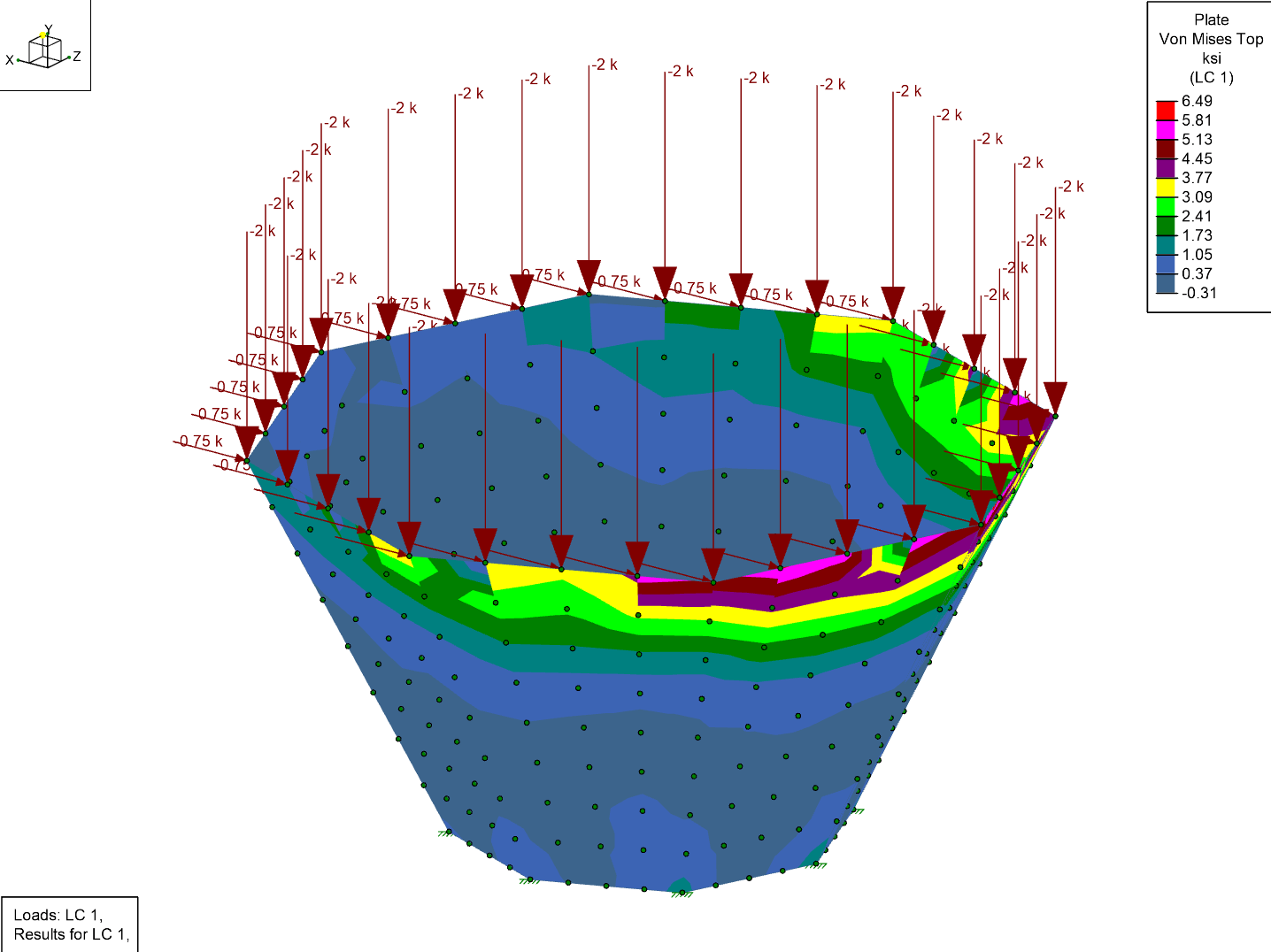
So, why not mesh the cone with 80 sides? After all, that should produce greater accuracy. However, you will find that the results don’t change much between the 40-sided cone versus the 80-sided cone. This is because you are converging on a theoretical correct solution. Furthermore, the 40-sided cone (which uses 200 plates) solves four times faster than the 80-sided cone (which uses 800 plates).
As a rule of thumb, if the results change by less than 10% when doubling your mesh you can probably stop submeshing at that point.

Transitioning plates from a circular (or elliptical) to a square (or...
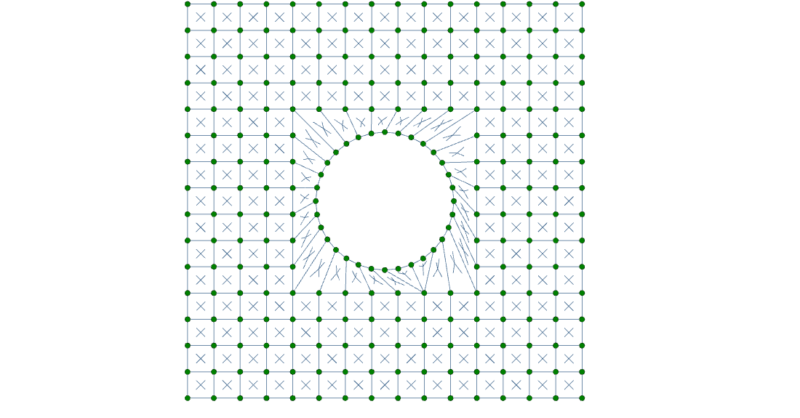
While RISA-3D (or RISA-2D) does not have an explicit tool to punch a...
It’s easy to apply tapered surface loads to plates in RISA-3D by...