When running a Response Spectrum analysis for seismic design, the response for high frequency modes can be included without solving for their individual mode shapes. This is often done to save analysis time and memory. This topic discusses some of the technical background and gives references for RISA’s implementation of this method.
Simple Overview
It can be difficult to achieve the 90% mass participation required by ASCE 7 for a response spectra / modal analysis. This is especially true for structures that have a large amount of mass at the lower levels of the structure. This mass will often be associated with very rigid modes. These modes may be so rigid that it may not be necessary to calculate the actual eigen modes. Instead, their response can be estimated accurately (and much more efficiently) using some simple estimates of their response.
This is done by figuring out what mass has been activated already with the currently solved eigen modes. This tells us where “missing mass” is that has not been activated. If one applies a response spectra acceleration equal to the zero period acceleration to this mass, then this should provide a reasonable estimate of the residual or missing mass.
RISA-3D Input
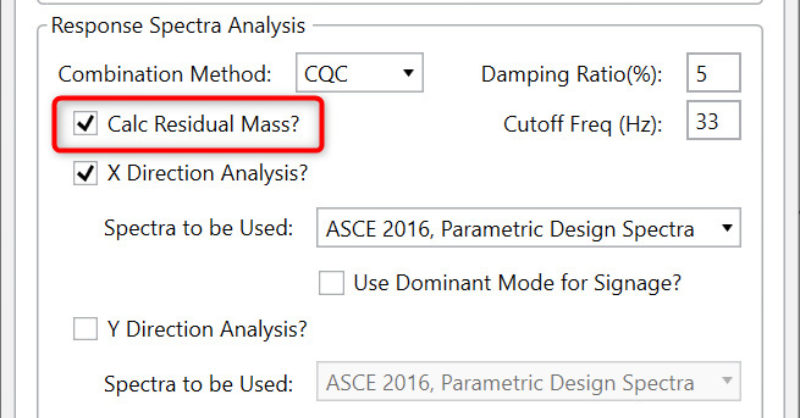
Version 13.0 of RISA-3D adds this capability into the Response Spectra Solution Options.
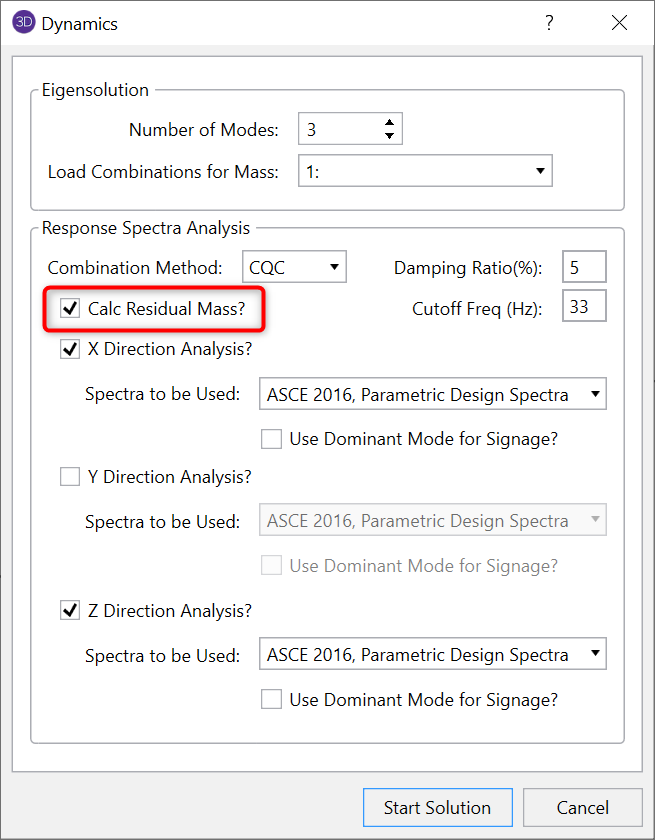
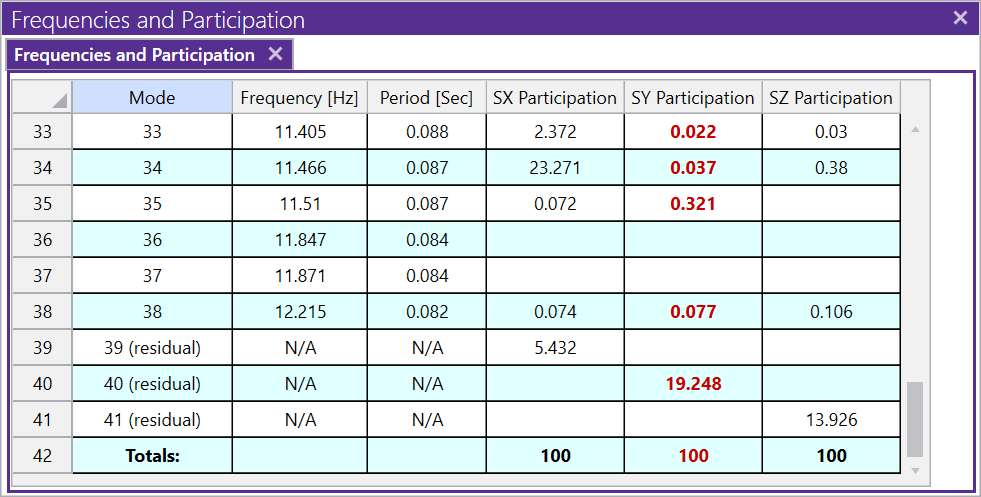
This option will add 3 additional modes above the numbers of modes directly requested by the user as shown below. The frequencies assigned to each mode are each 1 Hz above the previously solved mode. However, these frequencies are NOT used in the response spectra analysis at all.
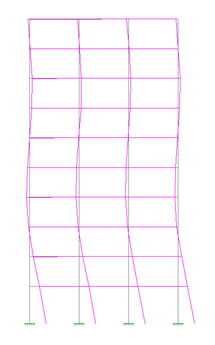
Displayed Mode Shapes
The modes produced by such an analysis will often look odd. This is because they tend to show displacement at the most rigid portions of the structures, such as the support locations. This is merely because the residual mass is located at these locations.
Rigid Response as an Extension of the Gupta Method:
Ajaya Kumar Gupta is one of the pioneers of the response spectrum method. His book (see image and link below) is one of best references on this method of dynamic analysis.
For years RISA has had an option to use his “Gupta Method” for the response spectra modal combination method. The theory behind this method is that modes higher than some rigid cutoff frequency (usually taken as 33 Hz) can all be considered to be acting in phase with each other. This means that the total response of these rigid modes can be expressed as the algebraic addition of their response rather than a statistical / probabilistic combination method like SRSS (Square Root Sum of Squares) or CQC (Complete Quadratic Combination).

In his book, Gupta, discusses how this concept can be extended even further, so that it may not even necessary to calculate the individual rigid modes. If all these modes are acting in phase with each other, why not just replace them with a single mode which represents their combined response. Because solving for eigen modes is so computational intensive, one could save a significant amount of solution time and memory by doing so. Since there isn’t a true frequency associated with this mode, one would assume that its response occurs at roughly the zero period acceleration (ZPA) of the response spectra. In RISA, the acceleration applied to the residual response is actually the highest spectral acceleration between the user entered cutoff frequency and the ZPA.
The (Painfully) Technical Details:
The ASCE-4 standard for the Seismic Analysis of Safety-Related Nuclear Structures and Commentary (see image and link to the left) has a number of code provisions specifically addressing the residual rigid response in a dynamic analysis.

It follows the same concepts described in the Gupta book. However, it may be useful to be able to reference a procedure published in a code standard using code language should a reviewer or building official ever challenge the validity of the Residual Rigid Response, or RISA’s specific implementation of it.
The Residual Mass Mode/Vector in ASCE 4 (and Gupta and RISA) is derived using the equation below, which merely subtracts out the directions response of existing modes from a unity vector for the direction under consideration.
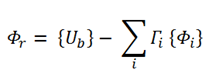
{Ub} is the static displacement vector obtained by displacing the base of the structure by unity.
{Φi} = the ith mode shapes
{Γi} = Modal Participation Factor
It would be possible to stop there just treat this residual mass mode as any other mode in the response spectra analysis. However, ASCE 4 (in equation 3.2-8) suggests calculating final response of this mode {Xo(max)} from the residual mass vector different than is done for true mode shapes. Instead, the response is calculated as a static solution to the equation.
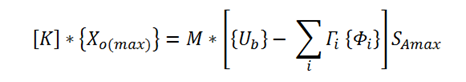
For this reason, this method is sometimes referred to as a Static Correction term rather than as a Residual Mass Mode. Regardless, when combining this static correction response with other modes it is treated the same as any other mode below the Gupta Cutoff frequency as described in item (f) of section 3.2.3.1 of ASCE 4.
Recommendations and Limitations
There are very few limitations with this method for seismic analysis. The residual rigid response can be effectively accounted for using this procedure in virtually all cases…at least within the context of response spectra analysis. The key caveat is that the response it represents should actually be the rigid response. For seismic, this generally means a value of at least 16 Hz, probably more like 33Hz. If the missing response has a significant periodic component, then the response will not be captured as effectively.