How to Run a Basic Dynamic Eigensolution in RISA-3D?

Welcome to a high-level walkthrough of dynamic analysis in RISA-3D! This guide introduces essential aspects of modeling dynamics, focusing on natural frequencies, mode shapes, and the impact of dynamic behavior on structural integrity.

The Dynamics Scenario

Imagine we’re tasked with evaluating the stability of a cantilevered pedestrian bridge that spans over a city street. The bridge is connected to a building on one side and features decorative panels and a lightweight canopy. The concern? Wind gusts and foot traffic could cause the bridge to vibrate. Our goal is to understand its dynamic properties—natural frequencies and mode shapes—and assess whether it can handle these dynamic forces without compromising structural stability.
We start by setting up dynamic mass for each load case:

1. 1. Canopy Load: Applied uniformly along the length of the bridge to account for wind effects.
   2. Pedestrian Load: Simulated at intervals along the span to reflect walking traffic.
   3. Decorative Panels: Modeled with specific weights on each side.

Once mass and stiffness are set, RISA-3D enables us to simulate how the structure behaves dynamically, revealing which parts might be sensitive to specific frequencies or forces.

Running the Eigensolution Analysis

In RISA-3D, we use an eigensolution to identify:

• Natural Frequencies (intrinsic vibration rates of the structure).
  

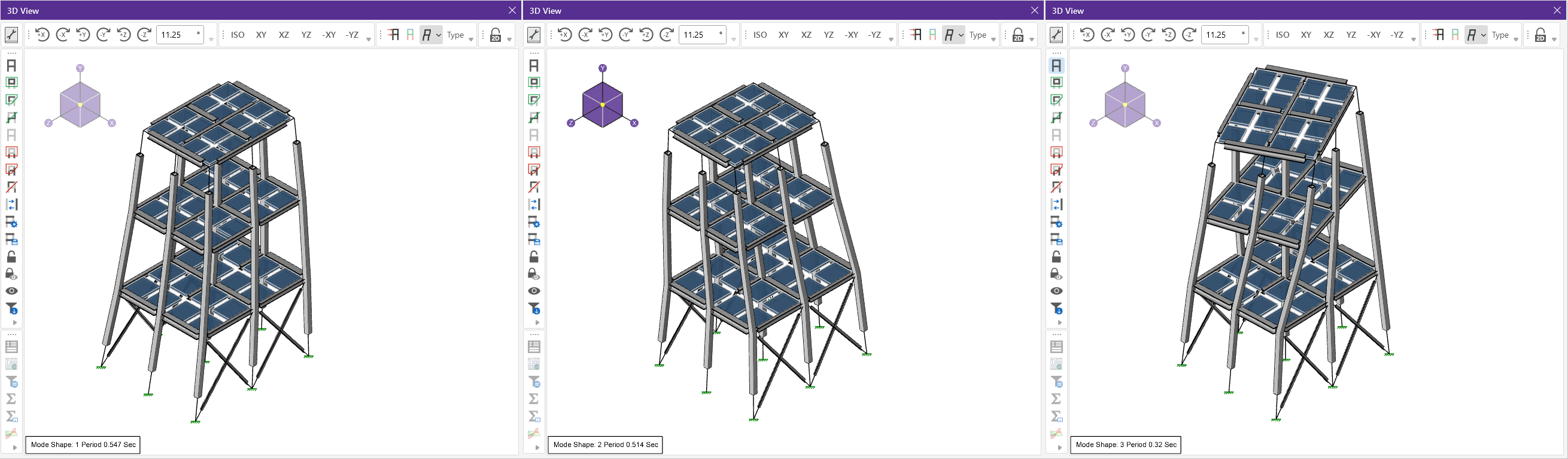
• Mode Shapes (distinct deformation patterns at each frequency).
  

To obtain accurate results, we create a load combination for dynamic mass and run the eigensolution. The output provides a table of frequencies, participation factors, and corresponding mode shapes. Here’s what we observe:

• Fundamental Mode: This first mode typically reflects the structure’s primary flexible response. For a cantilevered bridge, the first mode often involves vertical or horizontal sway.

• Mass Participation: If 85% of the mass participation is in the X-direction, it suggests a notable response to lateral forces in that direction, relevant for wind and pedestrian effects.

Interpreting Mode Shapes and Visualizing Results

Animating mode shapes in RISA-3D provides valuable insight into the bridge’s dynamic behavior:

• Mode 1: The entire bridge experiences lateral sway, which could resonate if subjected to sustained winds matching this frequency, amplifying movement and potentially stressing the connections.

• Higher Modes: Successive modes show stiffer responses, such as the structure bending at the cantilever support or in the canopy.

Through these animations, we see how each part of the bridge responds to dynamic forces. This analysis helps us consider mitigation strategies, such as:

• Structural Adjustments: Adjusting mass or stiffness, like reinforcing the canopy or adding dampers, to shift natural frequencies away from resonance with wind gusts.

• Further Analysis: Running a time-history analysis for specific traffic loading scenarios or a response spectral analysis for variable wind forces.

---

Troubleshooting: Recognizing and Resolving Localized Modes

Localized modes are a common challenge in dynamic analysis. These occur when only a small part of the model vibrates while the rest remains relatively still, often resulting in low mass participation. Here’s how to identify and mitigate localized modes effectively:

1. Spotting Localized Modes Localized modes can be hard to detect using frequency or numeric mode shape data alone but are easily recognized by using the mode shape animation feature. If only a small part of the structure moves while the rest stays still, it's likely a localized mode.

2. Impact on RSA Localized modes can reduce mass participation in RSA since they typically have little mass associated with them. This issue can be spotted if you notice minimal mass participation despite having a high number of modes.

3. Common Causes and Fixes Localized modes often stem from modeling errors, such as incorrect boundary conditions or unattached members. Try these solutions:

   1. Run a Model Merge: Always start with a Model Merge to address potential attachment errors or redundant nodes.
      
      

   2. Use Boundary Conditions: Adding a spring to a weak X-brace center can help restrain the mode shape and mitigate localized vibration.

   3. Adjust Material Properties: Making braces weightless prevents mass from concentrating in localized areas, reducing their impact on the eigensolution.

4. Delete Redundant Nodes: Removing nodes at brace intersections reduces degrees of freedom, minimizing flexible modes with low mass participation.

   Using Ritz Vectors When localized modes persist in models with plate or shell elements (e.g., walls or diaphragms), switch to the Ritz Vector dynamic solver. Ritz vectors prioritize modes with significant mass participation, reducing the prevalence of localized, low-mass modes.

Additional Resources
Have more questions about deflections in RISA-3D? Contact our support team or explore our Help File for further assistance.